The world around us contains a lot of stuff. Scientists say the Milky Way has 100 billion stars, that there are 2.5 million ants per human, and time says there will soon be 10 billion of us. Numbers like these are near impossible to conceptualize, making them very hard to reason about. How nice it is then, to speak of galaxies, colonies and populations—to speak of systems.

Systems offer a necessary tool to help fight this complexity, helping us to organize both the problem and solution space. They allow us to speak about collections of things as if they were part of one super-structure. Whether it’s a group of dishes in a meal, a group of players in a team or groups of body parts in a person, systems take a group of related objects and give us a simpler way of understanding them

In the following, I’d like to explore 5 patterns I’ve encountered in systems: language, list, link, lifecycle and processor.

Language

The language used at each level of a stratified design has primitives, a means of combination, and a means of abstraction.
Hal Abelson, Gerald Jay Sussman

Spoken language, written language, body language, programming language, musical language—each involves its own system of simple units that combine together to form richer structures. Languages help us to form expressions, meaningful phrases of content.

Perhaps the most concise definition of language comes from Abelson and Sussman’s SICP—that languages contain three mechanisms for expressing complex ideas: Primitives, Combination, Abstraction.

Primitive

Primitive expressions are the simplest elements in our language. These units, like words or notes, are the smallest pieces—lightweight and easy to put together.

We can think of primitives as the foundation that we build the language out of, as the expressible units that will be given order via combination and higher-order via abstraction, or as the leaves of grammar trees.

Combination

The “means of combination” allows us to build compound elements from simpler ones. Often, this combination follows certain rules for which primitives can be combined with others, and in what order.

We usually categorize our primitives into types, and establish rules for combination based on these types. In defining types and combination rules, we begin to flesh out a grammar.

Abstraction

The “means of abstraction” enables us to take a combination, and give it an identity as a higher-order primitive, for the purpose of later re-use. In these expressions, our primitives now draw from either simple primitive units or complex abstracted expressions.

The strength of language relies on this recursive nature, where parts can be built up and then treated as something simpler. Abstractions help to hide the mounting complexity of richer expressions by providing means of using fewer, simpler pieces to do construct .

In constructing or analyzing systems, we can make use of this pattern by enumerating the primitives, considering the rules for combination, and recognizing abstraction layers. Often, we will use typed units, grammars and recursion to accomplish these. For more on recursion, we’ll turn our attention to the next pattern: Lists.

List

Lists are a fundamental organization method within storage systems, defining a linear relationship between elements. In physical storage systems, we might put lists of papers in folders, lists of folders in boxes, and lists of boxes on shelves, shelves in warehouses, warehouses on streets, and so on. In digital storage systems, we similarly use folders, nesting these in file systems. As well, we use arrays of

Math offers us many ways to refer to lists: arrays, vectors, sets. Computer design pioneer Doug Engelbart used the famous phrase “thought vectors in concept space”, evoking the notion of lists in mental space. We can think of vectors as lists of things, and their grouping being a concept. In our homes, we can think of media vectors in shelf space, clothes vectors in closet space, or spice vectors in spice-rack space. Each of these arrangements allows us to categorize elements into a group, using the physical arrangement as a means of expressing something about the elements.

Perhaps chief among lists’ strengths are their recursive natures. The ability to nest lists within each other (like stacking shelves on top of each other) allows us to create layers of indirection and abstraction within large collections of elements.

The purpose of abstraction is not to be vague, but to create a new semantic level in which one can be absolutely precise.
Edsger Dijkstra

In general, we create new “semantic levels” to more accurately represent things. Using lists and recursion, we can form highly-expressive tree-shape. We saw this above with abstractions, which allowed us to build up trees of primitives and combinations, and then “nest” this within a richer expression, as an abstracted primitive.

Link

The human mind…operates by association. With one item in its grasp, it snaps instantly to the next that is suggested by the association of thoughts, in accordance with some intricate web of trails carried by the cells of the brain.
Vannevar Bush

While lists allow implicit, linear groupings, links allow for explicit, non-linear associations. While lists nest to create tree-forms, links are the basis of graphs. We can think of links as being the edges between nodes of information, forming combinations through connections and associations. Similar to Engelbart’s thoughts on thought vectors, another foundational figure in computing science, Vannevar Bush, used the metaphor of association (thought links) to describe mental processes.

In general, links used outside of our minds make use of addressing schemes to store “references” to linked objects. Links have long been a part of literature, directing readers to authors’ notes, references, definitions and so on. Page numbers can be considered a form of addressing, and indices and tables of contents as holding links to these addresses. In card storage systems like Zettlekasten, unique identifiers are attached to cards (units of content), and then used as a means of referencing cards, in the same way a website contains links to other sites.

These URLs, or Universal Resource Locators, are used to create references between web documents (hyperlinks). Whereas lists bring content together, links leave content in-place, instead “pointing” at linked content using addresses. In physical systems, the link merely provided direction—the reader still had to reposition themselves around to the new content. In digital systems, we can “select” links and be “jumped” to the new content, repositioning it around us.

A computer language should support the concept of ”object” and provide uniform means for referring to the objects in its universe.
Dan Ingalls

In Design Principles Behind Smalltalk, Dan Ingalls describes the need for objects in a computing system to have a uniform (and universal) means of reference. In more recent block storage systems like Notion, UUIDs are used to attach unique identifiers to “blocks” of content, which allows retrieval of and reference to that content. More generally, digital gardens combine both URLs and UUIDs to create linked systems of content, each document containing a bundle of pointers to both internal blocks (UUID-addressed blocks) and external content (URL-addressed web content). This enables the creation of rich, dense “hyperbundles” of links.

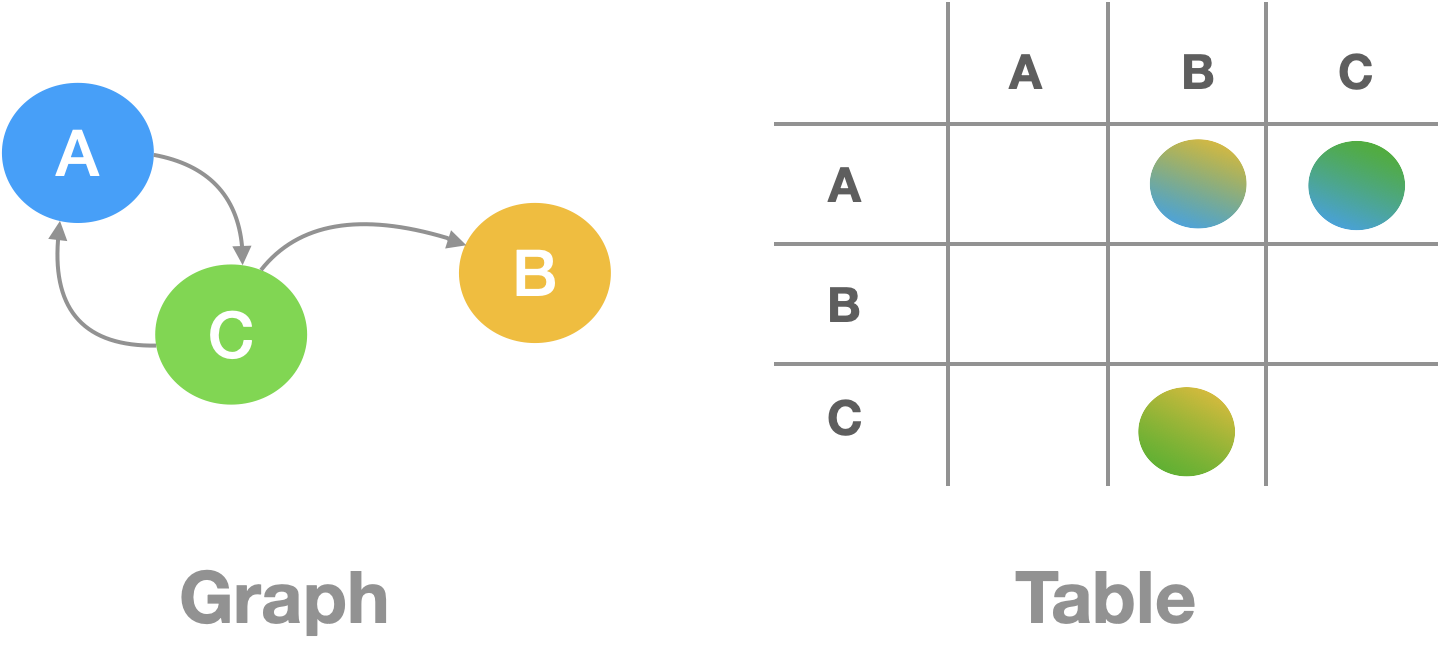
Links hold the great advantage over lists in not requiring an overarching hierarchy of nested objects. Instead, links build graph-shaped heterarchies, where elements have much freer association with each other. This allows for more flexible, less rigid structures.

Lifecycle

All the information that we create, collect, share and forget about can be thought of as participating in a lifecycle—birth, life, and passing. We can map these acts into four main phases in the life of a piece of information.

1. Capture: Bring a thing into our space
2. Describe: Give properties to the thingand relationships with existing things
3. Retrieve: Find and use the thing at a later time
4. Archive: Remove the thing to a separate space

Various fields in Information Science help to further articulate these.

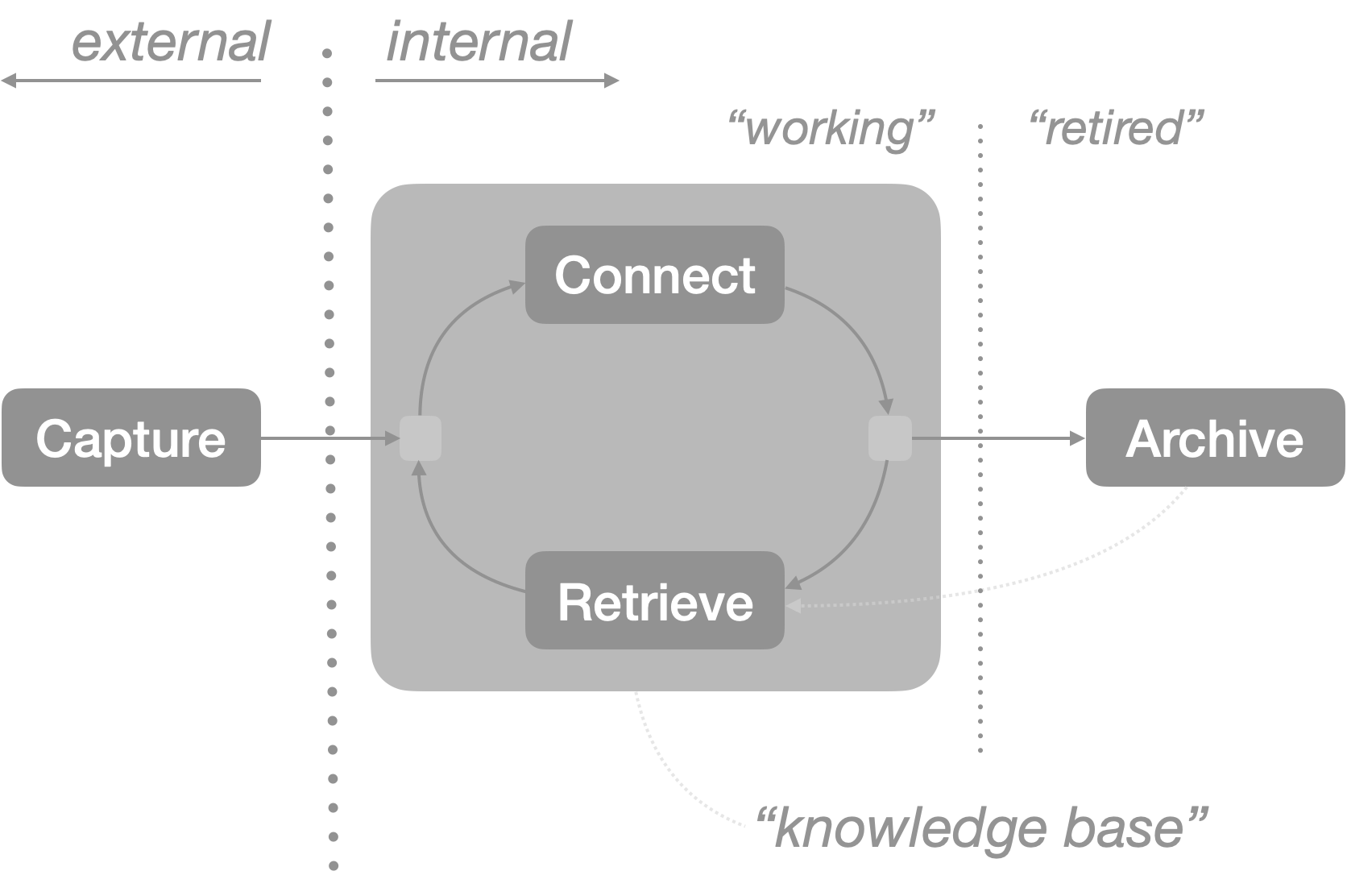
Capture

Information capture describes the process of intaking information, or bringing it into one’s information space. We can think of jotting down ideas, making sketches, collecting papers into folders, clipping sections from a newspaper, taking photos or recordings of our environment, or using the Share Button on our computing devices. The “capture” of this information involves more than simply acquiring, but also providing some means of initial organization so that it is properly contextualized upon entry into one’s information space.

Upon this entry, we are faced with a number of choices about how to sort a newly captured piece of information. Do we name it? Do we add annotations or notes? Do we put it amongst similar pieces of information? This is the work of descriptions.

Describe

At a high level, we can think about architecture as the design of spaces. Good architecture takes a set of needs, and arranges a set of rooms to satisfy those needs in a purposeful and pleasing way. Similarly, information architecture involves the structuring of information spaces to organize large bodies of information to facilitate easy and convenient access.

We can think of the same principles applied to one’s own information spaces. We often devise certain ways of describing items, such that we can find them among existing information, using metadata and relationships. The sorting of information into a location, in a folder, under a name, with notes or tags or links or with some other mechanism. Each represents a means of creating spaces (folder-space, namespace, tag-space) that information can occupy, be connected into, and retrieved from.

Each of these types of description can be thought of as a separate dimension in information space that the object lives on. We can both find objects by offering queries along these dimensions, searching in exact or fuzzy ways, and reveal similar objects, by exploring the dimensional neighborhoods around objects.

Retrieve

We go to the trouble of connecting information in part to make it easier to find again at a later time. Information retrieval involves the various methods used to search for content in our information spaces. In digital settings, we use a variety of retrieval methods—scrolling to a remembered location, browsing in a region, sorting and ordering, searching with text, filtering by date or other properties, following links, etc.

We often will attach metadata to digital assets in order to ease their retrieval. This metadata places the asset into a point along a dimension (time, color, size, alphabetical). By combining pieces of metadata, we can construct multi-dimensional arrangements of information. Provided we have the means to search/filter/sort along these dimensions, they serve to greatly aid the retrieval process by offering more methods of returning to an object, and finding similar objects.

Archive

Once a piece of information has finished being useful, it is archived in some capacity. This may involve marking it, storing it “off-site”, or discarding it entirely. Information management is concerned with the longer-running process of managing information through its entire lifecycle, ending with archival or deletion.

Often, we’ll not want to get rid of information, but move it out of our working space so that it doesn’t crowd the retrieval or connection of active information, keeping these processes efficient. We can think of an Active | Archive split in our information, with deleted information no longer existing.

A CRUDdy way to close

The lifecycle of most digital objects follows the CRUD mode: Create, Read, Update, Delete. We can break these down into existential (Create, Delete), transformational (Update) and presentational (Read) and map these phases to the four we explored above

• Create → Capture
• Read → Retrieve
• Update → Describe
• Delete → Archive

Processor

The final pattern, Processor, addresses the Input-Process-Output model followed in the units of most processing systems. In these systems, we take input, apply some process, and return an output. Each processing unit follows the same pattern, defining inputs and outputs of different shapes and types, and a process that maps inputs → outputs.

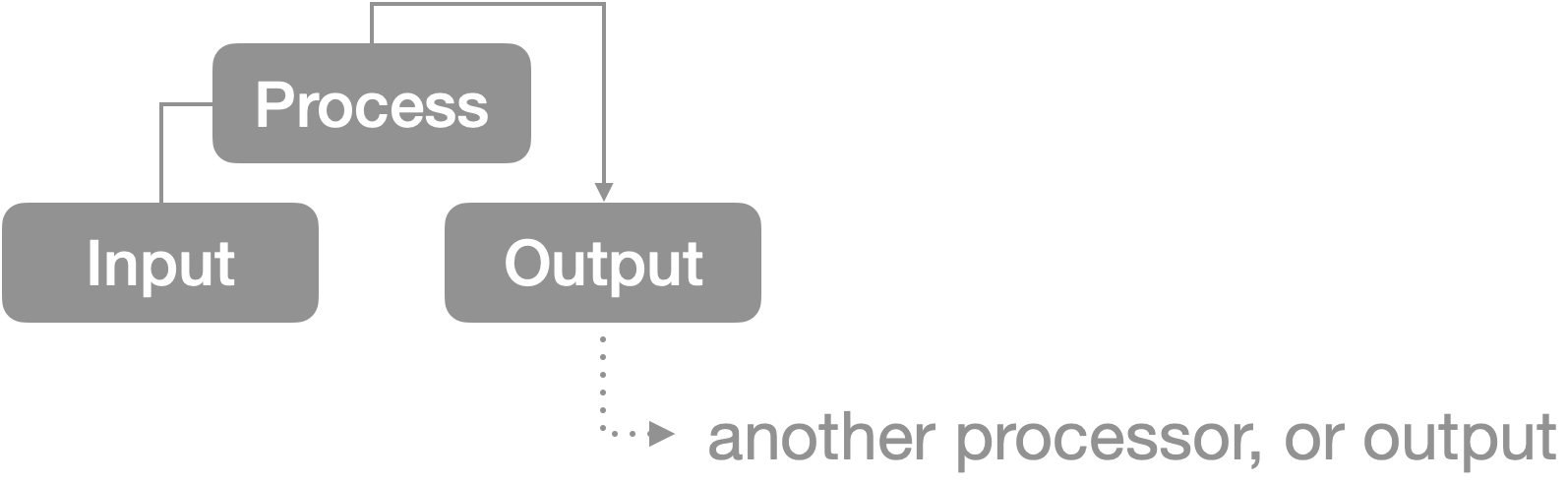
Systems of processors, thus, are concerned with process systems where the outputs of one processor are fed into the inputs of another. By connecting more processors together, we can do more complex processes. Through process primitives, we can decompose tasks into manageable chunks. Through process networks, we can execute tasks of arbitrary size. This balance of decomposition and composition gives processors their strength.

The most ready example might be baking and cooking, where in its simplest form, we take Inputs (ingredients), apply a Process (recipe), and return an Output (dish). More involved recipes might involve multiple such processes, in which dishes becoming ingredients for a higher-order dish.

This recursive nature is fundamental to processing systems—by feeding the results from one processing unit A to B, we create a higher-order processing units that can map the inputs of A to the outputs of B.

In analog and digital audio processing systems, chains of processors are constructed to perform various processing tasks. A simple model of this system involves making the inputs and outputs the same type—just audio signal data—so that processors can be rearranged in any sequence, while always outputting audio.

Recalling our above Language pattern, we can say that these processing units are the primitives in a processing language. We build grammars by combining them together, and define abstractions out of higher-order processes.

In order to accomplish this, we must design a) shapes for the primitives inputs and outputs, and b) rules for combination of outputs to inputs. We’ll tackle b) first, as our rules will simply be that to combine A→B, we must ensure that the outputs of A satisfy the inputs of B. That is, each input to B must be included in the outputs of A.

In thinking about a), we can consider the case of building processor systems in software. In these situations, we can think of a processing unit as a function, which takes in parameters, applies operations and returns a result (or results). Both the inputs and outputs will have a type, which defines the shape of the corresponding memory object in the software system. By defining parameters and returns to the function, we give the inputs and outputs shapes. In physical processor systems, these shapes might be defined by the plugs and ports each device presents.

Wrap Up

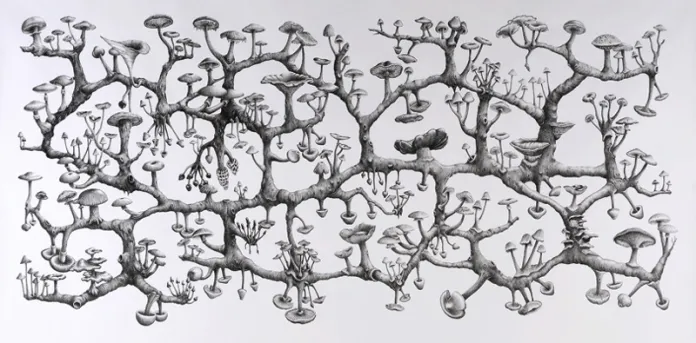
What I find most interesting about these patterns is that there is a lot of interplay between them. The basic forms of trees and graphs are present in each. These concepts of trees and graphs are addressed in many places, but perhaps most compelling for me is that of Deleuze and Guattari.

Using “rhizome” in place of graphs, they describe the tree as the “the paradigm for knowledge and practice in the modern Western world[,]…a coherent organic system that grows vertically and progressively”. In contrast, the rhizome is an “organism of interconnected living fibers that has no central point, no origin, and no particular form or unity or structure” (shown above).

Deleuze and Guattari argue that postmodern culture more closely resembles this form, with more freely intertwined interactions. Their argument, in itself, highlights the expressiveness of the tree and graph forms, serving as a cogent model for describing human behavior, as well as aspects of information, and much else.